八皇后问题
最近 Netflix 又出品了一部新剧,并在豆瓣上获得了 9.0 的高分,叫《后翼弃兵》。讲的是从小在孤儿院长大的主角拥有着不凡的国际象棋天赋,在她的天赋被发现挖掘之后一路走到了国际象棋世界冠军的故事。说到国际象棋,作为一名程序员,自然而然就想到了计算机的经典问题——八皇后问题。
所谓八皇后问题,就是在 8×8 的国际象棋棋盘上放置八个皇后,使得彼此之间不会互相攻击。一个皇后的攻击范围是皇后所在的行、列、和两条对角线上的所有位置,可以看成是加强版的中国象棋中的『車』,这就要求每两个皇后不能在同一行,不能再同一列,并且不能再同一条对角线上。维基百科上给出了一些可行解,例如下图所示,棋盘上有八个皇后,而这八个皇后互相攻击不到对方。
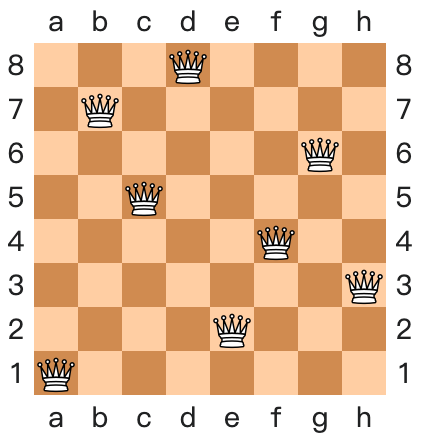
八皇后问题的一个可行解
并且百科中提到在 8×8 的棋盘上这样的解可以多达 92 个,那么如何才能找出所有的解呢?
首先想到的自然是穷举所有的情况,总共八列,每一列有八个格子,我们在穷举一遍每个格子,肯定能试出来所有的答案。这样确实可以,但搜索空间将会非常庞大,每一列是八种情况,八列总共会产生
种可能。当然对于现代计算机来说这不是一个很大的数字,但本着多快好省的原则总要问一句,还有更好的方法吗?
方法当然有,就是回溯法。回溯法本质上也是在试图穷举各种可能,但采取了一系列的判断条件来避免计算机去搜寻那些明显看起来就不可行的路径,当穷尽了当前路径的搜索之后,回到上一层,挑出下一个有可能有可行解的路径继续进行新的一轮搜索,这也是为什么管这种方法叫做『回溯』。撇开计算机程序,想象一下如果让我们人工解决这个问题,一个直观的想法就是在放置每个皇后之前,先判断一下这个位置能不能放,即同行、同列、同对角线上有没有其他皇后存在。如果都没有,就放置一个皇后,然后同样处理下一个位置。
直接语言叙述很难讲清楚,为了简单起见,这里我们用一个 4×4 的棋盘来举例说明回溯法是如何工作的。
从一个空白的棋盘开始,我们尝试放置第一个皇后,因为现在棋盘是空的,所以任何位置都是可以放的,那么直接放到第一行第一列(坐标 (1,1) )。
这时候第一行和第一列都被占了,根据国际象棋的规则, (2,2) 这个位置也不能放,所以第二行只能从 (2,3) 开始放置。这时的棋盘如下图所示。
这个时候我们发现,第三个皇后无论放在第三行的哪个位置,都会受到前两个皇后的攻击,所以这明显不是一条通路,所以回到上层发现,第二行还有一个可行的位置 (2,4) ,那么我们把第二个皇后放在该位置尝试一下。
很不幸,这个时候整个第三行也处于前两个皇后的攻击范围之内,而我们已经穷尽了第二行的所有可能性,这个时候只能回到第一行,尝试把第一个皇后放置到下一个允许的位置 (1,2) 上。
这时第二行只有一个可以放置皇后的位置 (2,4) 。
接下来把第三个皇后放到第三行的 (3,1) 。
第四行还有一个可行的位置 (4,3) 。
到此为止,我们就找到了一个『四皇后』问题的可行解。如果想要找到下一个可行解,需要以此回退到上一行,遍历下一个可以放置的位置,直到没有新的位置可搜索为止。
根据上述过程,我们可以大致写出如下的代码框架。输入参数 row 表示现在正在搜索第几行,因为两个皇后不可能出现在同一行,所以我们一次只处理一行的情况,放置完毕后,如果此行已经是最后一行,说明我们成功找到了一个可行解,否则继续搜索下一行。当下一行搜索完毕后,把当前行的皇后挪到下一个位置并重复上述过程。
def backtrack(row):
for col in range(4):
if can_place_queen(row, col):
place_queen(row, col)
if row == 3:
# we found a solution
else:
backtrack(row+1) # check next row
remove_queen(row, col)
目前还余下两个问题没有解决,一个是如何判断一个坐标能否放置皇后,即 can_place_queen(row, col) 函数,另一个是在棋盘上放置皇后和取走皇后的操作,即 place_queen(row, col) 和 remove_queen(row, col) 函数。
在实现这三个函数之前,先定义我们用来表示棋盘的数据结构。对于皇后的位置,我们只需要记录下它们的坐标即可,而我们最感兴趣的是如何能快速判断一个位置是否处于已经存在的皇后的攻击范围之内,我们当然可以维护一个二维数组作为棋盘,给出一个坐标,检查当前行的每个位置,当前列的每个位置,以及两条对角线上的每个位置,但这样需要花费不少时间去一个个的检查,这无疑拖慢了程序的速度。那么有没有一个快速的方法达到相同的目的呢?
在这里我去参考了一下 LeetCode 上的讲解,发现对于一个矩阵而言,一条从左上角到右下角对角线上的所有坐标的横纵值之差是固定的,用上面的例子举例, (1,1), (2,2), (3,3), (4,4) 四个坐标都处于这条对角线上,而它们的横纵值之差都为 0 ;类似地,一条从右上角到左下角对角线上的所有坐标的横纵值之和是固定的,比如说 (1,4), (2,3), (3,2), (4,1) 这四个坐标,它们的横纵值之和都为 5 。这样只需要维护两个数组结构就能表示给定坐标的两条对角线上有没有其他皇后存在。
所以可以定义这样四个数据结构分别表示皇后的位置,某列上有没有皇后,两条对角线上有没有皇后,
queens = set()
cols = [False] * 4
dale_diagonals = [False] * (2 * 4 - 1)
hill_diagonals = [False] * (2 * 4 - 1)
我们不必关心每行的情况,因为 backtrack 函数一次只处理一行,一个已经放置了皇后的行是不可能会被放置第二个皇后的。
这样就能很容易得出暂时缺失的三个函数。
def can_place_queen(row, col):
return not cols[col] and not hill_diagonals[row-col] and dale_diagonals[row+col]
def place_queen(row, col):
queens.add((row, col))
cols[col] = True
hill_diagonals[row-col] = True
dale_diagonals[row+col] = True
def remove_queen(row, col):
queens.remove((row, col))
cols[col] = False
hill_diagonals[row-col] = False
dale_diagonals[row+col] = False
把它们组合到一起,一个完整的『四皇后』问题解决代码就完成了。
def can_place_queen(row, col):
return not cols[col] and not hill_diagonals[row-col] and dale_diagonals[row+col]
def place_queen(row, col):
queens.add((row, col))
cols[col] = True
hill_diagonals[row-col] = True
dale_diagonals[row+col] = True
def remove_queen(row, col):
queens.remove((row, col))
cols[col] = False
hill_diagonals[row-col] = False
dale_diagonals[row+col] = False
def backtrack(row):
for col in range(4):
if can_place_queen(row, col):
place_queen(row, col)
if row == 3:
# print solution
# where dot represents empty cell
# and 'Q' represents queen
for row, col in sorted(queens):
print("." * col + "Q" + "." * (4-col-1))
else:
backtrack(row+1) # check next row
remove_queen(row, col)
queens = set()
cols = [False] * 4
dale_diagonals = [False] * (2 * 4 - 1)
hill_diagonals = [False] * (2 * 4 - 1)
backtrack(0)
同样的思路也可以扩展到 N 皇后问题上,将表示棋盘大小的 4 替换为其他数字即可。
那么回溯法的搜索空间是多大呢?还是以 4×4 的棋盘为例,第一行显然有四个位置可以放置皇后,而第一行的皇后使得第二行至少有两个格子处于它的攻击范围之内,因此第二行至多有 4-2=2 个可用位置,以此类推,第三行至多有一个位置,第四行也至多有一个位置。因此搜索空间为 4×2×1×1 = 8 ,较之以前的确小了不少。
这样推导到更通俗的情况,对于 N×N 的棋盘,回溯法的搜索空间为 N×(N-2)×(N-4)×…×1 = O(N!) 。对于开头提到的八皇后问题,时间复杂度就降到了 。
